可伸缩性是衡量应用程序加速比多少的尺度之一(注:加速比指应用程序串行化与并行化之间所花费时间之比,它表示并行化之后的效率提升结果)。2 倍的加速比表明并行程序仅需要花费串行程序的一半时间。比如理想情况下,运行在单处理器上的程序花费 30 秒,而在双核机器上运行仅需花费 15 秒。
我们总是期望运行在双核机器上的应用程序要比在单核上快的多。同理,运行在四核机器上也要比在双核上快的多。这就好像以前当 CPU 换代升级时,随着主频提升,我们的程序总是可以运行的更快。很不幸,大多数应用程序在步入多核时代后,性能不但没有提升,甚至有所降低。
假如我们增加更多的处理器核心数,而应用程序并没有获得额外的加速。从这点来看,该应用程序不具有可伸缩性。如果强制使用另外的处理器核心,通常会造成性能下降。因为这时分布式和同步的开销开始凸显威力。
更多关于可伸缩性的指导方针,楼主强烈推荐这篇文章:可伸缩性原则。
应用程序到底有多少并行性可言?
如小标题所说,应用程序到底有多少并行性呢?答案是视情况而定(废话)。
显然,这个问题取决于解决问题的多寡和发现并恰当利用并行算法的能力。我们先前大部分讨论(更多讨论请参见:并行思维 [I])都围绕着如何在昂贵和稀有的并行计算机上编写高性能程序。随着多核处理器时代的到来,许多方面已经发生变化。我们需要退一步来重新审视一下。
Amdahl 定律
Gene Amdahl 发现在计算机体系架构设计过程中,某个部件的优化对整个架构的优化和改善是有上限的。这个发现后来成为知名的 Amdahl 定律。该定律告诉我们,假如我们以 2 倍加速程序的全部,那我们可以预期程序运行的比 2 倍更快。但是,假如我们只以 2 倍加速优化程序的一半,那么整个系统只改善了 1.33 倍。Amdahl 定律很容易可视化表达。设想有个程序由 5 个相同的部分组成,且每个部分运行时间均花费 100 秒,如图 1 所示:
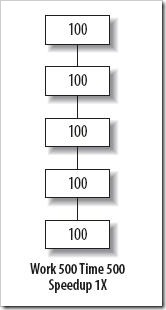 图 1
图 1
如果我们以 2 倍和 4 倍来加速其中的两部分,如图 2 所示:
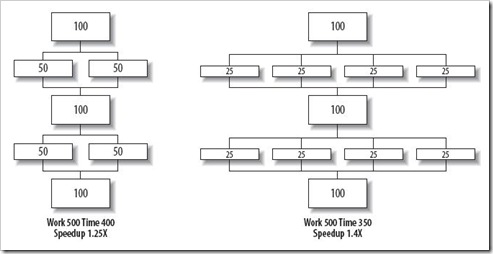 图 2
图 2
那么程序运行总时间将由原来的 500 秒分别缩减至 400 秒和 350 秒。 但是,我们也应该看到,更多的部分不能通过并行来加速。无论有多少处理器核心可用,串行部分 300 秒的障碍都不会被打破,如图 3 所示:
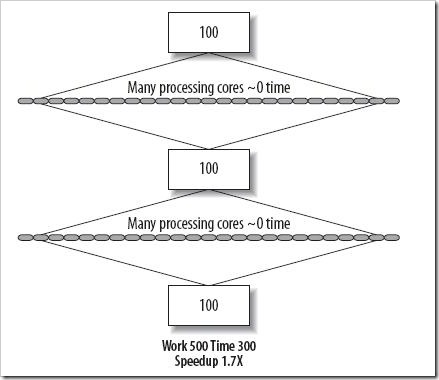 图 3
图 3
上述最终表明,无论我们拥有多少处理器,都无法让程序非并行(串行)部分运行的更快。
并行程序开发人员可以利用 Amdahl 定律来预测使用多少处理器来达到最大的加速比。Amdahl 定律是个悲观定律,但业界还有另外一种视角来看待该问题,这就是接下来要讲述的 Gustafson 定律(注:至于 Amdahl 及 Gustafson 定律的计算公式,大家可以 Google 之)。
Gustafson 定律
Sandia 国家实验室的 John Gustafson 从一个不同的视角来重新审视 Amdahl 定律。他指出并行非常有用。因为随着计算机越来越强大,应用程序会聚焦在更多工作上,而不是一个固定工作量。今天的应用程序几乎都不运行在 10 年前的老机器上,甚至也很少运行在 5 年前的机器上。而且这并不局限在游戏领域,它同样适用于办公软件,Web 浏览器,图形图像处理软件,以及像 Google Earth 此类的软件。
其实,Amdahl 定律本身做了几个假设,尽管这些假设在现实世界中不一定正确。第一个假设就是最优串行算法的性能严格受限于 CPU 资源的可用性。但是实际情况并非如此,多核处理器可能会为每个核实现一个单独的 Cache,这样,Cache 中就能够存放更多的数据,从而降低了存储延迟。Amdahl 定律的第二个缺陷就是它假定串行算法是给定问题的最优解决方案。但是,有一些问题本质上就是并行的,因此采用并行实现时所需的计算步骤就会比串行算法减少很多。
Amdahl 定律还有更大的缺陷,也就是第三点假设,关于问题规模的假设。Amdahl 定律假设在处理器核数量增长的时候,问题的规模保持不变。这在大多数情况下不成立。一般来讲,当给予更多计算资源的时候,问题规模都会随之增大以适应资源规模的扩大。对于很多问题来说,随着问题规模增长时,需要解决的并行部分比非并行部分(即串行部分)增长的更快速。因此,随着问题域增长,串行部分所占比例减少。参照 Amadahl 定律,程序可伸缩性得到增强。
仍然以 图1 为例。假如问题随着可用并行性伸缩,我们就能看到如图 4 所示:
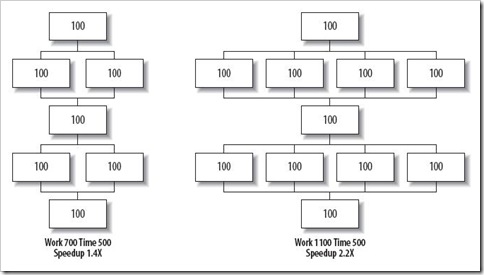 图4
图4
如果串行部分仍然花费相同的时间量,随着其在整体中所占比例的下降,变得越来越不重要。最终的结果便如图 5 所示,程序性能随着处理器数量线性增长,复杂度为 O(n)。
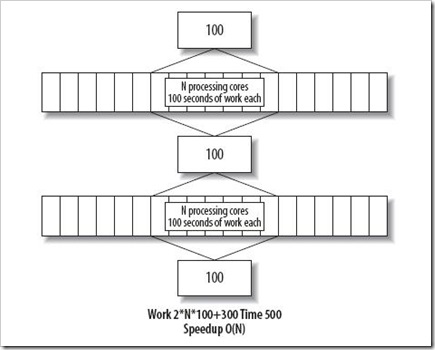 图5
图5
即便如此,程序的性能仍然非常受限于串行部分。投入了大量处理器只为那 40% 的效率提升。这在超级计算机上,无疑是恐怖的浪费。在多核处理器系统上,我们当然希望其他工作也能并发运行,以便能充分利用未能利用的处理能力。这是更加复杂的新世界。
无论我们采用 Amadahl 定律视角还是 Gustafson 定律视角,在任何情况下,最小化串行代码都是良好的习惯。这两大定律的观点也都是正确的。不同之处在于你想要程序在既有工作量的前提下运行的更快,还是更快速的处理更大的工作量。不过实践表明程序越复杂,要解决的问题规模越大。Gustafson 定律更加符合现实一点。尽管如此,Amadahl 定律仍然时刻困扰我们,如果你要在相同基准下,让单一程序运行的更快。
通过切换到并行算法而不扩展问题规模,从而使得应用程序运行的更快。这通常比在更大的问题规模上使其运行更快困难的多。应用程序的可伸缩性可以归纳为并行化增长的工作量和最小化串行工作。Amadahl 定律促使我们努力减少串行部分,而 Gustafson 定律则告诉我们要考虑更大的问题域。尤其是相对串行工作来说, 并行化增长的工作量。
串行化算法 VS 并行化算法
有一个很明显的事实是:最佳串行化算法很少是最佳并行化算法,反之亦然。这意味着要使程序在单核,多核系统上都运行良好,仅仅编写良好的串行代码或并行代码并不够。
超级计算机程序员从实践中得知,并发任务工作量会随着问题规模的功能快速增长。假如工作量的增长比串行化开销(例如通信,同步)还要快,那么仅通过问题规模的增长就可以判定程序可伸缩性不佳。程序不会说在 100 个处理器下可伸缩性不佳,而到了 300 个处理器下可伸缩性就变好了。
该如何应对多核的到来?很简单,放弃过去的串行思维,开始并行思考。


