等优曲线的特征有四:第一,它的斜率为负,即向右下方倾斜。大家翻回到 64 页的图 3-1 ,刚才我们已经分析过这图上的四个点,知道 A 点一定优于 D 点,因此把 A 、 D 两点连接起来的向左上方倾斜的线不可能是一条等优曲线。事实上,大家想象一下,如果 X 、 Y 商品都是越多越好的物品,增加其中一种商品的数量而还要保持效用不变,当然就要减少另一种商品的数量才行,所以效用一样的商品组合的点,肯定是沿着这两种商品一增一减的方向移动才有可能构成一条等优曲线出来。既然一种商品增,另一种商品减,则这条曲线的斜率当然是负的。
第二,两条等优曲线永不相交。这个用数学上的反证法就能证明。大家看书上 71 页的图 3-6 。先假设有两条相交的等优曲线 U1 与 U2 ,它们交于 A 点。由于 A 点与 S 点同在 U1 的等优曲线上,即 A 点与 S 点等优;又由于 A 点与 T 点同在 U2 的等优曲线上,即 A 点与 T 点等优。根据前述的传递性公理,必有 S 点与 T 点等优,则这两个点应该位于同一条等优曲线上,但事实是它们位于两条不同的等优曲线上,这说明前提错误,两条等优曲线是不可能相交的。
第三,直角坐标系上每个点都有等优曲线通过(这称为“等优曲线的完备性”)。这其实等价于前述的比较公理,由此可推出平面上实际上密密麻麻地分布着无数条等优曲线,并不是书上 70 页画的那样只有几条——这是因为如果把所有等优曲线都画出来,整个平面就会是一片漆黑——,或者可以这么说,每两条等优曲线之间总可以再画出一条等优曲线来,这跟两个实数之间总可以再找到一个实数是类似的逻辑。同一条等优曲线上的点的效用(使用价值)是一样的,但不同等优曲线上的点的效用(使用价值)当然是不一样的。那怎么比较大小呢?结论是:越远离原点的等优曲线被称为位置越高的等优曲线,所代表的效用水平(使用价值)就越高。这结论的证明如下:再看回书上的 64 页的图,假设 B 、 C 两点是位于同一条等优曲线上的,显然可以再通过 A 点画一条等优曲线,位置比 B 、 C 所在的那条更远离原点;也可以通过 D 点画一条等优曲线,位置比 B 、 C 所在的那条更靠近原点。前面我们已经分析过, A 点优于 B 、 C 两点,所以 A 点所在的那条较远离原点的等优曲线所代表的效用水平(使用价值)较高;而 B 、 C 两点都优于 D 点,所以 D 点所在的那条较靠近原点的等优曲线所代表的效用水平(使用价值)较低。
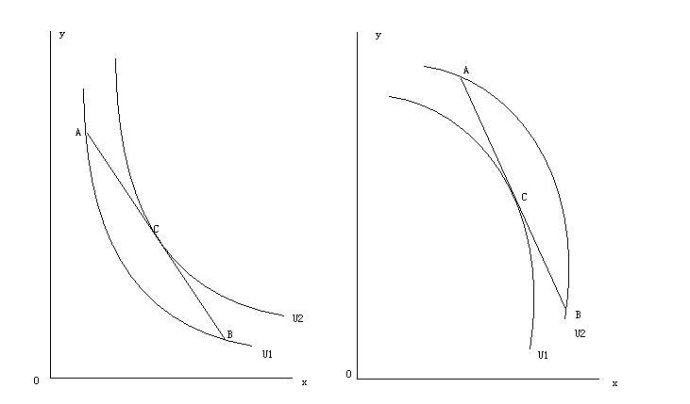
第四,等优曲线凸向原点。等优曲线是向右下方倾斜的曲线,但 71 页的图 3-7 的左图与右图都是向右下方倾斜,可是形状并不一样,左图是凸向原点,右图是凹向原点。左图含义着人喜欢“消费多样性”,而右图则含义着人喜欢“消费单一性”。大家看我在黑板上画的图,左图里有一条 U1 的等优曲线,上面有 A 、 B 两点,把这两点以直线连起来,取中间的 C 点,过这 C 点可以作另一条 U2 的等优曲线,而 U2 所代表的效用水平(使用价值)是高于 U1 的,也就是 C 点的效用高于 A 、 B 点。显然, C 点的商品组合中两种物品的数量都比 A 、 B 点的商品组合要均衡。这连接 A 、 B 点的直线后面我们就会学到,是两种物品的(相对)价格线(预算线),也就是在某一价格水平下,人会认为均衡地消费两种物品,比极端地消费其中一种物品(如 A 点是过多地消费 Y 商品, B 点是过多地消费 X 商品)更为优胜。反之,右图里也有一条 U1 的等优曲线,上面也有 A 、 B 两点,把这两点以直线连起来,取中间的 C 点,过这 C 点也可以作另一条 U2 的等优曲线,但这时 U2 所代表的效用水平(使用价值)是低于 U1 的,也就是 C 点的效用低于 A 、 B 点。这说明在某一价格水平下,人会认为极端在消费其中一种物品,比均衡地消费两种物品更为优胜。显然,现实里的人的行为支持的是左图那种凸向原点的等优曲线。